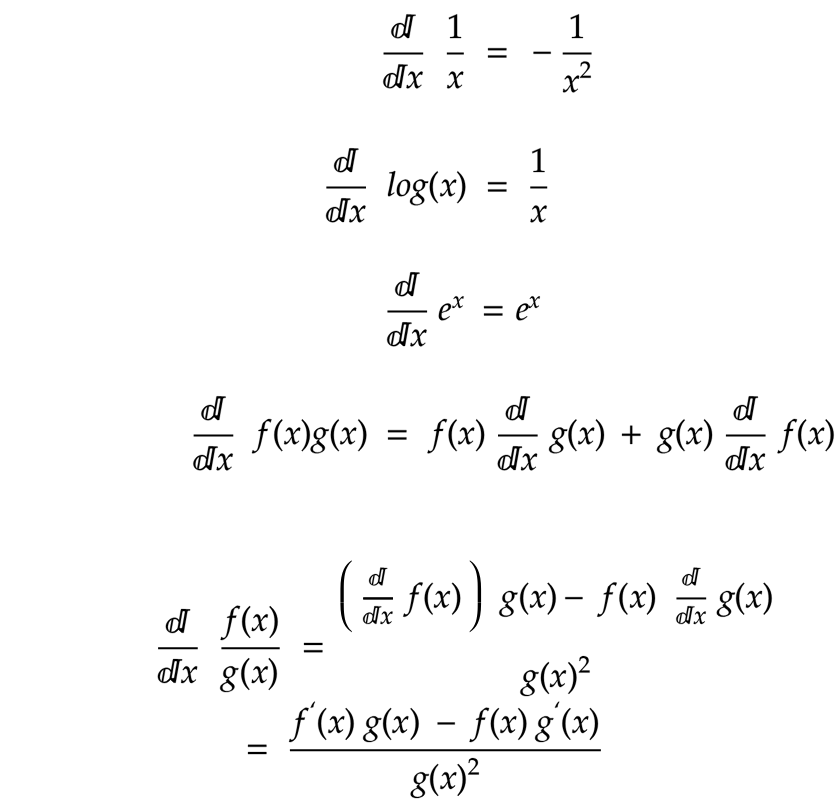
Sigmoid helps to bring the inputs between [0, 1], used most of the classification problems. eg; regression, neural network etc.

Speciality of tanh function is it brings the inputs into [-1, 1], some cases this range is important especially RNN, where the model want to selectively forget things.

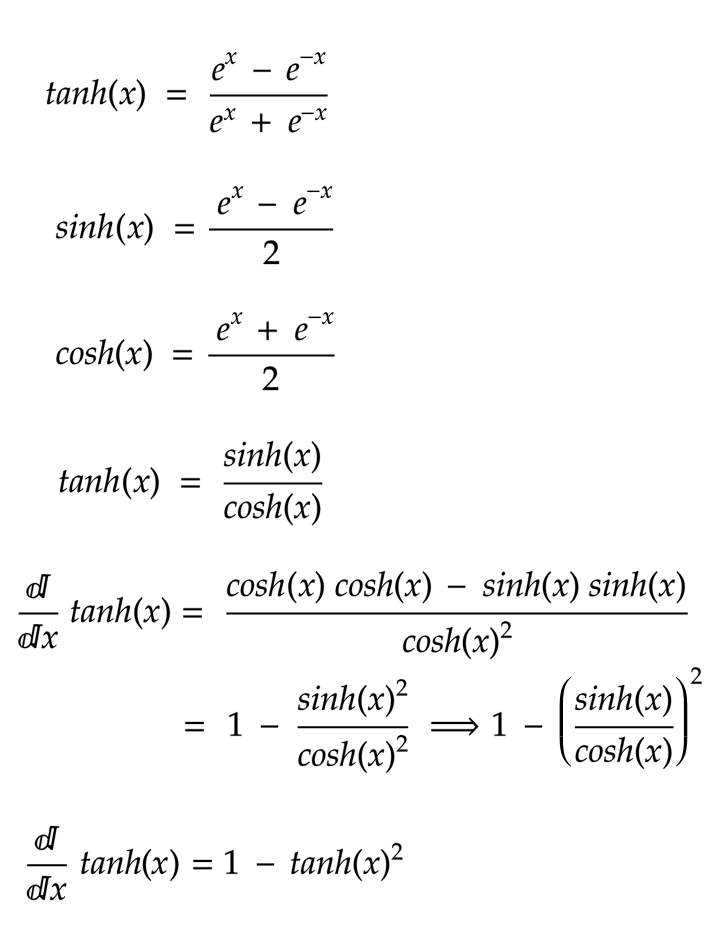
Widely used activation function in Neural network and CNN models. This activation function helps the Deep learning jump in multiple domains. As early days getting a proper activation function was really restricting complex neural network architectures.

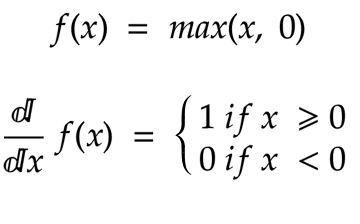
Improved version of Relu which reduces the chance of vanishing gradient issue.

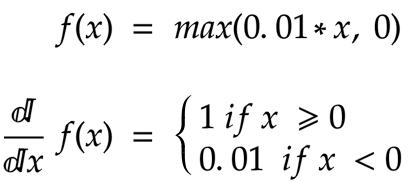
Used mainly as last layer in nerual network. This function helps to bring all activations from previous layer into probability values. Because of this property this function used most of the classification problems.

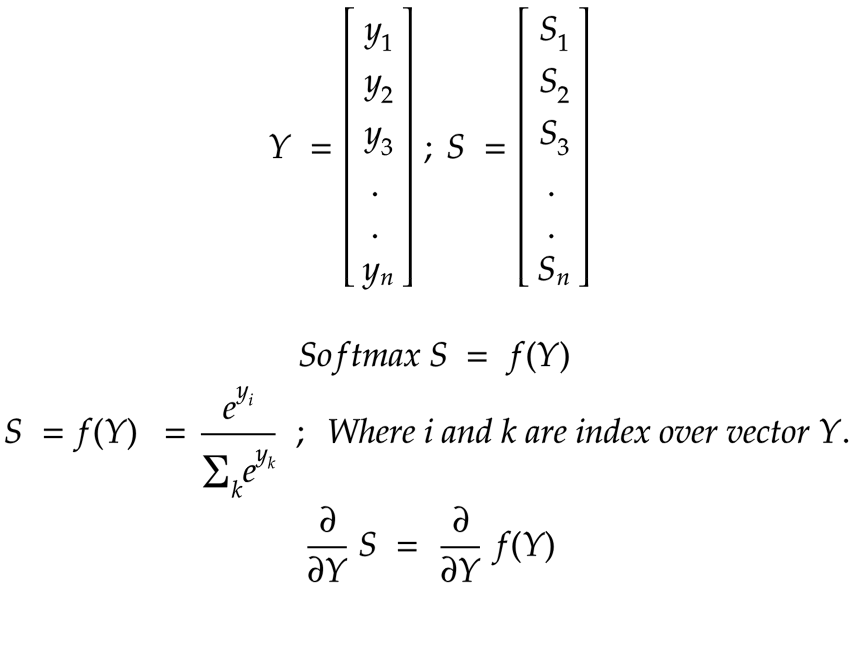
Objective function used in neural network or classification problems.

This concept are learned in undergrad courses. All ML problems are finally comes to numerical optimization problem. Derivatives plays a method to optimize the parameters of the function. We required partial derivatives to find derivative of multi-varite equations.

The key idea is, at every step we calculate the derivative of one-dimention or (one variable) keeping all other variables constant.